Singular Value Decomposition (SVD: 특이값 분해)
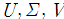 에 대하여 임의의 rank k인 m x n 행렬
에 대하여 임의의 rank k인 m x n 행렬  는 다음을 만족한다.
는 다음을 만족한다.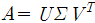
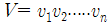 은
은  를 orthonally diagonalize 한다. V 의 column vector는
를 orthonally diagonalize 한다. V 의 column vector는  의 Eigenvector 이다.
의 Eigenvector 이다. 들이
들이  의 Eigenvalue라고 하면,
의 Eigenvalue라고 하면, 의 diagonal element들은
의 diagonal element들은  를 만족한다. 여기서
를 만족한다. 여기서  을 만족한다.
을 만족한다. 벡터 집합을 고려해 보면,
벡터 집합을 고려해 보면,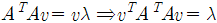 이므로
이므로 ,
,  이다.
이다. 이성립한다. 따라서
이성립한다. 따라서 는 k개의 영이 아닌 벡터로 이루어진 A의 열공간의 직교 집합이다. 즉, 열공간의 직교 기저가 된다. 이들 벡터를 Normalize하여 열공간의 정규직교 기저를 얻으면,
는 k개의 영이 아닌 벡터로 이루어진 A의 열공간의 직교 집합이다. 즉, 열공간의 직교 기저가 된다. 이들 벡터를 Normalize하여 열공간의 정규직교 기저를 얻으면,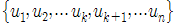 의 정규 직교 기저를 얻을수 있다. (정규 직교 기저는 차원을 확장 하는게 가능하다 k->n )
의 정규 직교 기저를 얻을수 있다. (정규 직교 기저는 차원을 확장 하는게 가능하다 k->n )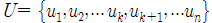 라 하고,
라 하고, 로 U를 구할 수 있다.
로 U를 구할 수 있다.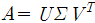 =
=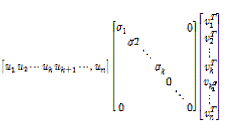


댓글남기기