Hidden Markov Model (HMM) - 1

Markov model

* markov 특성 : ex 영어에서 Q자 다음에 U자가 많이 나오는 현상이 통계적으로 밝혀져 있다. 따라서 U자가 나타날 확률은 U자 앞에 나타난 알파벳에 영향을 받는다는 것을 짐작 할 수 있다. 이렇듯 메시지나 사건들이 이전의 상태에 영향을 받는 것이 Markov 특성이라고 한다.

* markov process : 미래의 프로세스가 현재의 상태에 의해서만 결정되는, 즉 과거와는 독립적인 랜덤 프로세스를 마르코 프로세스라고 한다.

 

markov process는 크게 두 가지로 나뉜다.

 

3.1 MM(Markov model)

: 어떤 state를 지나가는지 알 수 있고 상태의 순서나 어떤 결정함수(deterministic function)를 알 수 있다.

 

아래 출처로부터 이해하기 쉽게 정리된 그림들을 가져왔다.

 

출처:

http://blog.daum.net/_blog/BlogTypeView.do?blogid=09dDw&articleno=15605818&categoryId=967326&regdt=20080406104610#ajax_history_home

 

문제) 오늘 날씨가 sunny 인 경우, 다음 7일의 날씨 변화가(state sequence)가 'sunny-sunny-rain-rain-sunny-cloudy-sunny' 일 확률은?

 

 

근데 condition으로 있는 model 은 무엇이지? 가끔 확률 공식을 보면 이런식으로 수식을 계산하는데 배경으로 깔려있는 조건 전체를 지정하기도

한다. 이는 관측 데이터에 따른 state transition probability , first-order Morkov Assumption 등등을 통칭하는 의미라고 할 수 있다.

 

 

위 수식을 이용하면 8일째 맑을 확률을 알 수 있을 것이다.

 

그런데, 왜 시간 T=t에서 상태 i인 모든 path( state sequence)의 확률을 전부 더한게 T=t 에서 날씨(state)가 i 일 확률일까?

간단히 생각하면, P(A OR B) = P(A) + P(B) 이기 때문이다.

 

그러나, 위의 알고리즘 대로라면 Time complexity가 N과 t에 기하급수적으로 증가하므로 다음의 Dynamic programming 기법이 제안된다.

 

* Dynamic programming : 최종 계산하고자 하는 과정중 중복되는 계산이 있으면 이를 매번 계산 하지 말고 메모리에 저장해놨다가 필요할 때 다시 사용하여 계산 량과 시간을 줄이는 방법

 

여기서 aji는 상태 j에서 상태 i로의 전이 확률(transition probability)이다. 즉, 모델의 prior probability(사전 확률) 이다.

prior란 우리가 이미 알고 있는 사실을 기반으로 어떤 확률을 계산할 때, 그 알고 있는 사실을 나타낸다고 할 수 있다.(?)

 

 

 

3.2 HMM(Hidden Markov Model)

 

: 어떤 state를 지나는지 알지 못하고 단지 어떤 확률적인 function 만 알 수 있다.

* HMM은 출력치만 관측 되고 상태의 흐름은 관측 되지 못한 경우에 사용된다.

 

MM의 경위 위와 같은 형태로 모델을 구성할 수 있다.

 

그러나, HMM의 경우 State에 대한 정보(초기상태, aij , bij)를 알 수 없다.

이 정보를 model parameter  라고 하자.

 

우리가 알고 싶은 관심사는   이다. 그러나 우리가 알고 있는 사실은 관측 데이터 X들이다.

따라서 우리는 알고 있는 정보 X를 이용해 Model parameter   를 구해야 한다.

 

이를 풀기 위한 기본 notation

 

 

 

 

B는 j state가 Vk라는 관측 데이터를 뱉어낼(?) 확률 이다.

 

1st order markov assumption은 MM이나 Markov chain에서도 언급했던 가정이다.

 

이 이론에서 더 나아가 conditional independency of observation parameter는

관측된 데이터는 이전의 state와 무관하고 오직 관측된 시점의 state로부터 기인한다는 가정이다. 이도 markov assumption과 같은 맥락이라고 생각하면 될 것 같다.

 

이러한 가정들로부터 모델을 간단화 시킬 수 있다.

 

 

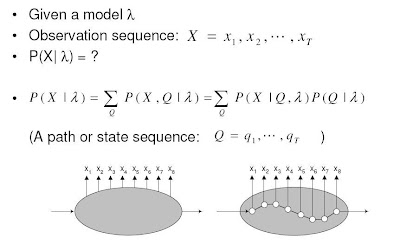
그림으로 예를 들어 설명하자면,

 

Q는 state(path) sequence 이다.

 

위의 수식대로, 우리는 관측된 X로부터 가장 그럴싸한 Q를 구해 내는 것이 목표이다.

이 문제를 풀기 위해서 Viterbi algorithm 과 em algorithm을 이용 한다.

이는 나중에 알아보기로 하고 일단은 output sequence의 확률을 state sequence를 이용해 나타내 보자.

 

 

 

* output sequence가 X일 때 그에 대응 하는 path sequence는 굉장히 많다. 그러나 확률로 표현하면, 이 모든 path sequence들로부터 나오는 output의 합이 우리가 관찰한 output sequence라고 할 수 있다.

이 수식은 다음과 같이 model parameter를 이용해 풀어 쓸 수 있다.

 

위의 방식 또한 Dynamic programming을 쓰지 않으므로 개선의 여지가 있다.

 

Dynamic programming을 사용한 Forward algorithm과 Backward algorithm이 있다. 

다음 포스팅 에서 이를 다룬다.

http://cheezestick.blogspot.kr/2012/09/hidden-markov-modelhmm-2.html