1. 고유값과 고유 벡터
참고 : http://doctory.egloos.com/10224327
A를 하나의 Square matrix라고 하면 x vector에 대해 다음과 같이 쓸 수 있다.
우변의  는 상수이며 A의 고유값 이라고 한다.
는 상수이며 A의 고유값 이라고 한다. Square matrix A와 vector x의 곱(우변)이 상수  와 vector곱으로 표현(좌변)되었으므로,
와 vector곱으로 표현(좌변)되었으므로, Vector x가 A에 의해 선형변환이 되면 A의 고유값인 상수  만큼 scale의 변화만 가지는 영역으로 표현 된다는 의미이다.
만큼 scale의 변화만 가지는 영역으로 표현 된다는 의미이다. 이때, 두 영역 모두에서 고유한 값을 가지는 vector x가 고유 값이라고 한다.
(고유벡터들은 서로 직교 한다. 그리고 일반적으로 normalize된 값으로 표현한다)
좌변에서는 고유 벡터 x의 회전변환을 A 행렬이 가할 수 있지만, 우변에서는 단지 상수  에 의해서 고유 벡터의 스케일의 변화만 있을 수 있다.
에 의해서 고유 벡터의 스케일의 변화만 있을 수 있다. 그렇기 때문에 변환된 space에서는 변하지 않는 일정한 axes(기저)를 고유 벡터를 통해 나타 낼 수 있다.
A가 symetric 한 성질을 가지고 있으면 다음과 같이 A를 고유 분해 할 수 있다.
D: Eigen value 를 diagonal하게 가지는 행렬
임의의 B행렬이 있을 때  라면
라면 그러면 A의 Eigen Vector U는 unitary matrix이다.
(unitary matrix : 모든 성분이 서로 orthogonal 하고, 각 성분은 normalized)
unitary matrix는 다음과 같은 성질을 가진다.
즉 symmetric한 행렬 A는 다음과 같이 분해 될 수 있다.

 는 상수이며 A의 고유값 이라고 한다.
는 상수이며 A의 고유값 이라고 한다. 와 vector곱으로 표현(좌변)되었으므로,
와 vector곱으로 표현(좌변)되었으므로, 만큼 scale의 변화만 가지는 영역으로 표현 된다는 의미이다.
만큼 scale의 변화만 가지는 영역으로 표현 된다는 의미이다. 에 의해서 고유 벡터의 스케일의 변화만 있을 수 있다.
에 의해서 고유 벡터의 스케일의 변화만 있을 수 있다.
 라면
라면
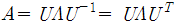


 는 상수이며 A의 고유값 이라고 한다.
는 상수이며 A의 고유값 이라고 한다. 와 vector곱으로 표현(좌변)되었으므로,
와 vector곱으로 표현(좌변)되었으므로, 만큼 scale의 변화만 가지는 영역으로 표현 된다는 의미이다.
만큼 scale의 변화만 가지는 영역으로 표현 된다는 의미이다. 에 의해서 고유 벡터의 스케일의 변화만 있을 수 있다.
에 의해서 고유 벡터의 스케일의 변화만 있을 수 있다.
 라면
라면
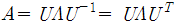

댓글남기기