SVM (Support Vector Machine)
1. What is the SVM ?
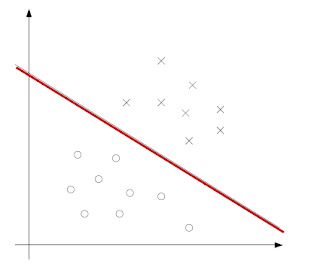
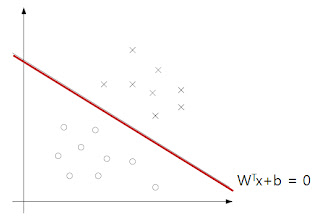
Hyperplane은 다음과 같이 수식적으로 표현 될 수 있다.
 ........................(1)
........................(1) 라고 쓸 수 있으며 X 벡터는 additional한 1을 가진다. 두 식을 전개 해보면 그 이유를 알 수 있다. 다음을 보자
라고 쓸 수 있으며 X 벡터는 additional한 1을 가진다. 두 식을 전개 해보면 그 이유를 알 수 있다. 다음을 보자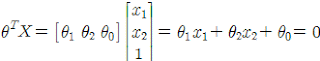 되고 이식을 정리 하면
되고 이식을 정리 하면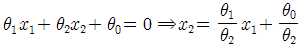 이 된다.
이 된다. 이고 y 절편이
이고 y 절편이  인 직선이다. 이는 차원이 n차원으로 늘어나도 똑같이 적용 된다.
인 직선이다. 이는 차원이 n차원으로 늘어나도 똑같이 적용 된다. 그러므로
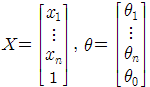 가 된다.
가 된다.
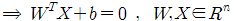 ........................(2)
........................(2)
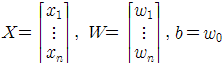
이렇게 정의된 hyperplane은 test data(=unseen data)를 다음과 같이 분류 할 수 있다.
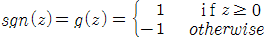
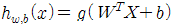 ................... (3)
................... (3)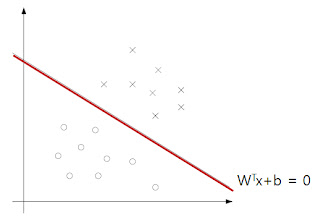
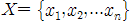 이라는 test data가 들어왔을 때, 식(3)에 vector X를 넣었을 때, hyperplane보다 위쪽 영역에 위치하면
이라는 test data가 들어왔을 때, 식(3)에 vector X를 넣었을 때, hyperplane보다 위쪽 영역에 위치하면 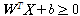 이므로 , h(x)는 1이 되고 아래쪽 영역에 위치하면
이므로 , h(x)는 1이 되고 아래쪽 영역에 위치하면  이므로 h(x)는 -1이 된다.
이므로 h(x)는 -1이 된다.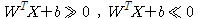 일 경우에는 confident 하게 test data를 구분 할 수 있다.
일 경우에는 confident 하게 test data를 구분 할 수 있다.* 추가 개념 1. Hyperplane과 벡터 W는 항상 서로 orthogonal 하다. 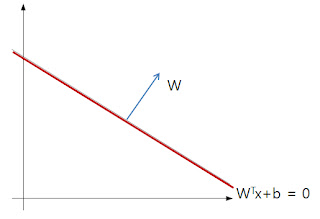 2차원의 Hyperline으로 이를 보이자면,  일 때 일 때Hyperline(2차원이므로 line이라고 일컫겠다)  는 기울기벡터 는 기울기벡터  을 가지고 있다. 을 가지고 있다. 이다. 서로의 내적값이 0 이므로 두 벡터의 사이각은 90도가 이다. 서로의 내적값이 0 이므로 두 벡터의 사이각은 90도가됨을 알 수 있다. 차원이 증가해도 이러한 성질은 동일하므로, N차원의 hyperplane과 n차원의 벡 터 W는 항상 직교함을 알 수 있다. |
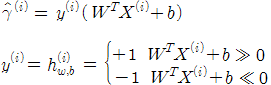 ...................... (4)
...................... (4)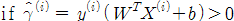
2.3 Geometric margin
2.2에서 functional 하게 margin을 정의 해보았다. 이번에는 Geometric Margin을 생각해보자. (이하 G-Margin)
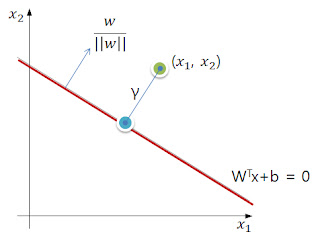
 좌표에 위치 하고 있다. (
좌표에 위치 하고 있다. (  : position of data) 그 데이터와 hyperplane
: position of data) 그 데이터와 hyperplane  과의 euclidean distance가
과의 euclidean distance가  라고 하자.
라고 하자.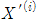 (
(  ) 을 다음과 같이 알 수 있다.
) 을 다음과 같이 알 수 있다. 이 식을 정리 하면
이 식을 정리 하면  값은 다음과 같다.
값은 다음과 같다.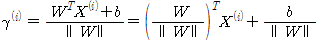 이 식의 결과는 positive training example 에만 적용이 된다. negative의 경우 값이 음수가 되기 때문에 이를 막기 위해 다음과 같이 정의 한다.
이 식의 결과는 positive training example 에만 적용이 된다. negative의 경우 값이 음수가 되기 때문에 이를 막기 위해 다음과 같이 정의 한다. .................. (5)
.................. (5)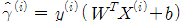 .................. (4)
.................. (4) ................... (5)
................... (5)3 The optimal margin classifier

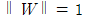 이라는 constraint는 모든 상황에서 항상 유효하지 않다 (non-convex) 그러므로 optimal margin classifier를 구하기 위해서는 F-Margin 대신에 G-Margin을 이용한다.
이라는 constraint는 모든 상황에서 항상 유효하지 않다 (non-convex) 그러므로 optimal margin classifier를 구하기 위해서는 F-Margin 대신에 G-Margin을 이용한다. ............ (6)
............ (6) 은
은  로부터 만든 constraint 이다.
로부터 만든 constraint 이다.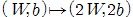 과 같이 일정한 배수배로 조정을 해도 hyperplane의 성질이 변하지가 않는다. 그 이유는 식(3)에서 정의한
과 같이 일정한 배수배로 조정을 해도 hyperplane의 성질이 변하지가 않는다. 그 이유는 식(3)에서 정의한  의 값은 sign값에 의해 결정되지 magnitude에 의해서 결정되는 것이 아니기 때문이다.
의 값은 sign값에 의해 결정되지 magnitude에 의해서 결정되는 것이 아니기 때문이다. 를 적절히 조절해서
를 적절히 조절해서 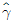 = 1 로 설정 할 수 있다는 이야기다.
= 1 로 설정 할 수 있다는 이야기다.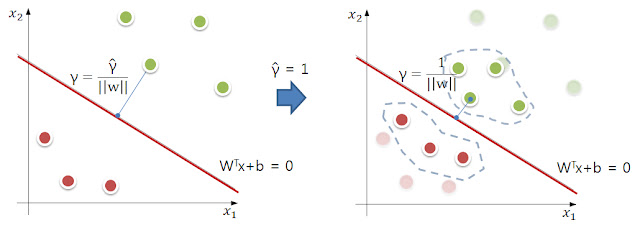
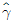 = 1 로 설정해도 오른쪽처럼 전체적인 변동은 있지만 hyperplane은 동일한 역할을 수행한다.
= 1 로 설정해도 오른쪽처럼 전체적인 변동은 있지만 hyperplane은 동일한 역할을 수행한다. 으로 정의 하는 것은, 뒤에 나올 primal optimization problem 과 연관이 있는 듯하다 (아마 문제를 정의하기 유리한 form이기 때문일 것이다.) <- 이부분은 뒷부분이 공부된뒤 다시 기입
으로 정의 하는 것은, 뒤에 나올 primal optimization problem 과 연관이 있는 듯하다 (아마 문제를 정의하기 유리한 form이기 때문일 것이다.) <- 이부분은 뒷부분이 공부된뒤 다시 기입
............. 이 부분은 optimization을 공부 하고...
naive하게 적어보자면
Lagrange duality를 이용해, vector를 support vector들과의 inner product로 표현 가능하게 변환 시킬수 있다.
이렇게 변환 하게 되면, kernel을 적용 하기에 유리한 모양이 되므로
kernel trick을 이용할 수 있게 되고, 보다 다양한 mapping function을 적용 할 수 있게 된다.

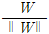
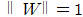
댓글남기기