PCA(Principal Component Analysis) 주성분 분석
이를 통해 데이터를 효과적으로 압축 할 수도 있고, 그 데이터에 대한 잡음과 불필요한 성분을 제거한 Principal 한 components들을 정의 할 수 있어, 얼굴인식등과 같은 응용에 PCA가 활용 될 수 있다.
1.1 Find a pattern of the data
데이터의 특성을 뽑아내기 위해선 먼저 데이터 간의 관계를 알아야 한다.
이를 위해서 데이터의 covariance matrix를 이용한다.
covariance matrix를 통해 데이터의 특성을 알기 위해서는, covariance matrix의 Eigen value와 Eigen vector를 구해야 한다.
1. 고유값과 고유벡터에서 말했듯이. Eigen value와 Eigen vector는 어떤 변환 matrix의 특성을 나타낼 매우 중요한 기준이 되기 때문이다.
2차원 영역에 대해서 간단한 예를 들면,
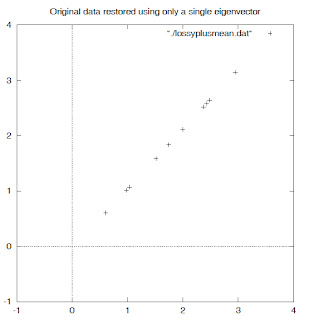
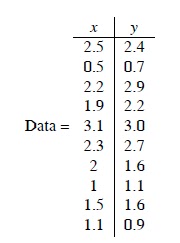
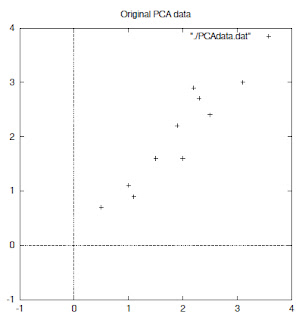
와 같은 데이터가 있다고 하자. 그 데이터는 오른쪽 그림과 같이 2차원 영역에 점으로 나타낼 수 있다.
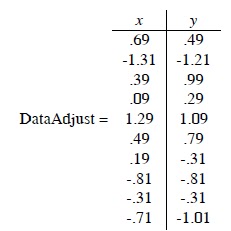
데이터의 정규화를 위해서 기존의 데이터에서 각각 영역의 평균값을 빼 다음과 같이 데이터를 refine해주면, (기준을 0,0으로 맞춰줘야 데이터를 다루기 편함)
위의 2차원 데이터에 대해 covariance matrix를 구하면 2X2의 matrix를 구할 수 있다.
이 Matrix에 대해 Eigenvector와 Eigenvalue를 구할 수 있다.
직관적으로 생각해 봤을 때, Eigenvalue의 값이 크면 그 큰 Eigenvalue로부터 생성된 Eigenvector가 생성하는 기저 축에 데이터의 패턴, 성질의 표현이 많이 되어있다고 생각 할수 있다.
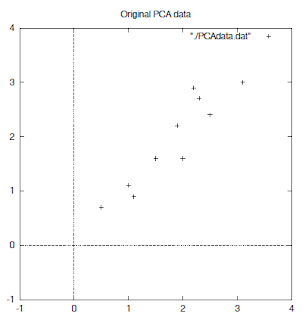
egienvector를 데이터 그래프에 plot해보아도 이 사실을 알 수 있다.
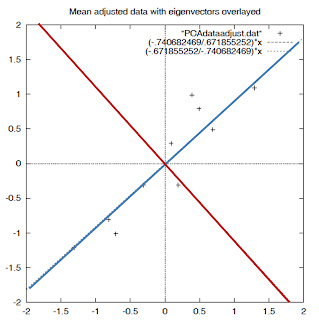
파란색선과 빨간색 선은 eigenvalue로부터 구해진 eigenvector들이며 이들은 새로운 space의 기저(기준 axes)를 나타낸다. 이 둘은 normalize가 되어있고 서로 직교 한다.
그림을 보면 확인 할 수 있겠지만, 데이터들이 주로 파란색 axis를 따라 분포 하고 있다.
(파란색 선이 1.28402771의 eigenvalues 의해 생성된 eigenvector 이다.)즉 위의 예에서 두 개의 eigenvalues 중 데이터에 대해 더 많은 정보를 가지고 있는 것은 파란색 벡터이며 이는 가장 큰 eigenvalues로부터 구해진 값이다.
이를 생각해보면, 데이터의 성질을 파란 eigenvalue 와 eigenvector가 많이 나타내고 있으므로 차원을 해당 vector를 이용해 줄이게 되면 효과적으로 데이터를 표현 할 수 있다.
빨간색 라인에 의해 결정되는 성분은 필요에 따라 잡음으로 간주해 제거 할 수도 있고, 데이터의 pattern 표현에 주요한 영향을 미치지 않기 때문에 무시함으로써 데이터를 효과적으로 압축 할 수도 있을 것이다.
이러한 성질을 이용해, 주요 기저(파란색)만을 이용하여 데이터의 차원을 줄여 다음과 같이 표현 할 수 있다.
Feature Vector = 
feature vector는 데이터에 대한 정보량이 많은 eigenvector이다.
변환된 데이터는 다음과 같다.
이는 x,y로 표현되던 데이터가 x로만 표현 되었으므로 2차원에서 1차원으로 차원이 낮아졌다.
이렇게 표현된 데이터를 다시 원래의 영역으로 나타내기 위해 다음과 같은 과정을 거친다.
FeatureVector는 EigenVector이므로 orthogonal한 Vector이므로 역함수와 transpose와 같으므로,,,
이를 그래프로 나타내면,
즉, 한라인 위에 데이터들이 모두 사영(?)이 되었다
원본의 데이터와 비교해 봤을 때, 정보량을 무려 절반(2차원->1차원)으로 줄였음에도 불구하고, 대체적으로 기존의 성질을 유지 하고 있다. (물론 기존의 data set이 PAC에 유리한 분포를 가지고 있었던 것은 사실이다.)
이러한 일련의 과정으로 주어진 data set을 효과적으로 dimension을 줄여 표현 할 수 있다.
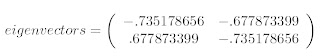
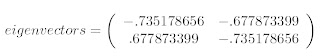
댓글남기기