A compact algorithm for rectification of stereo pairs
1. Introduction
두 이미지간의 Matching Point(이하 대응점) 찾기는 컴퓨터 비전의 몇몇 분야에서 필수적이다.
보통의 이미지 Pair에서 서로간의 대응점을 찾기 위해서는 왼쪽의 어느 한 point와 오른쪽의 모든 point를 빠짐없이 비교해야 되기 때문에 계산 량이 매우 많을 수 있다.
Rectification을 통해 이러한 문제를 어느 정도 해결 할 수 있다.
다음 그림을 보자.
그림 2를 일련의 transformation을 통해 그림 4를 얻을 수 있다.
이 과정을 통해 찾고자 하는 대응점들이 수평 한 라인 위에 위치하게 된다.
그렇게 되면 그림 3에서의 어느 한 점에 대한 그림 4의 대응점을 단지 해당하는 horizontal line만 검사하여 찾을 수 있다.
즉, 계산 량은 다음과 같이 줄어든다.
2. Camera Model
두 개의 카메라 View를 가지는 camera model은 Fig 1. 로 나타낼 수 있다.
Fig 1에 표시된 점들은 다음과 같다.
W : 실제 오브젝트의 위치
C : 카메라 pinhole의 위치
R : Image plane
M : 오브젝트가 image plane에 사영된 점
E : Epipole
3. Epipolar Geometry and Rectification
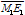 ,
, : Epipolar line
: Epipolar line
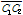 : Baseline
: BaselineFig 2.와 같이 Epipolar line과 base line을 평행하게 함으로써 Image 들을 rectification 할 수 있다.
Fig 2의 오른쪽 그림을 보면 알 수 있듯이 이때엔 더 이상 epipole이 존재 하지 않는다.
이때의 Epipolar line은 line at infinity 이다.
rectification 된 새로운 image plane Pn1 과 원래의 image plane Po1의 관계를 구할 수 있다.
이는 다음과 같은 식으로 구해질 수 있다.
새로운 R은 Epipolar geometry를 이용해 구해 질 수 있다.
r1은 x축으로서 baseline과 평행하다.
r2, r3 는 각각 다른 축들과 orthogonal 하다
r2 를 구하기 위해서는 r3 가 필요한데 아직 새로운 값을 수하지 못했기 때문에 이전의 r3 값을 old plane의 것을 사용한다.
k는 즉 old plane의 r3 값이다.
우리는 이로서 mn1와 mo1의 관계식을 얻을 수 있다. 같은 방법으로 mn2와 mo2 의 관계식도 얻을 수 있다.
4. Example
그림 5의 위쪽 그림들은 원본 이미지이고 아래 이미지들은 Rectified 이미지 이다.
Rectified 이미지의 epipolar line이 평행해 졌고 왼쪽의 대응점들과 라인이 일치하는 것을 확인 할 수 있다.
위 매틀랩 프로그램은 다음과 같이 기술 되어있다.
%-----------------------------------------------
function [T1,T2,Pn1,Pn2] = rectify(Po1,Po2)
% RECTIFY: compute rectification matrices
% factorize old PPMs
[A1,R1,t1] = art(Po1);
[A2,R2,t2] = art(Po2);
% optical centers (unchanged)
c1 = - inv(Po1(:,1:3))*Po1(:,4);
c2 = - inv(Po2(:,1:3))*Po2(:,4);
% new x axis (= direction of the baseline)
v1 = (c1-c2);
% new y axes (orthogonal to new x and old z)
v2 = cross(R1(3,:)’',v1);
% new z axes (orthogonal to baseline and y)
v3 = cross(v1,v2);
% new extrinsic parameters
R = [v1’'/norm(v1)
v2’'/norm(v2)
v3’'/norm(v3)];
% translation is left unchanged
% new intrinsic parameters (arbitrary)
A = (A1 + A2)./2;
A(1,2)=0; % no skew
% new projection matrices
Pn1 = A * [R -R*c1 ];
Pn2 = A * [R -R*c2 ];
% rectifying image transformation
T1 = Pn1(1:3,1:3)* inv(Po1(1:3,1:3));
T2 = Pn2(1:3,1:3)* inv(Po2(1:3,1:3));
% ------------------------
function [A,R,t] = art(P)
% ART: factorize a PPM as P=A*[R;t]
Q = inv(P(1:3, 1:3));
[U,B] = qr(Q);
R = inv(U);
t = B*P(1:3,4);
A = inv(B);
A = A ./A(3,3);
%-----------------------------------------------
참고 및 출처 :
출처 : A compact algorithm for rectification of stereo pairs
Andrea Fusiello1, Emanuele Trucco2, Alessandro Verri3
1 Dipartimento Scientifico e Tecnologico, Universit`a di Verona, Ca’' Vignal 2, Strada Le Grazie, 37134 Verona, Italy; e-mail: fusiello@sci.univr.it
2 Heriot-Watt University, Department of Computing and Electrical Engineering, Edinburgh, UK
3 INFM, Dipartimento di Informatica e Scienze dell’'Informazione, Universit`a di Genova, Genova, Italy
Received: 25 February 1999 / Accepted: 2 March 2000
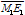 ,
, : Epipolar line
: Epipolar line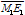 ,
, : Epipolar line
: Epipolar line
댓글남기기